

Science makes it known,
Engineering makes it work,
Art makes it beautiful.
D .dll, Silverfrost FTN95, and Numerical Recipes:
The Art of Scientific Computing1
(Simulated Annealing2) - FORTRAN Files
(alternatively, Mathematical Procedures - FORTRAN Files)
This is the second part of D .dll (dnrprocs.dll) calling
a FORTRAN .dll (mathproc.dll). This page focuses on
mathproc.dll Simulated Annealing
related subprograms.
The FORTRAN Simulated Annealing related subprograms
called by dnrprocs.dll
are contained in mathproc.for (compiled and linked into
mathproc.dll; mathproc.for also contains other
engineering, scientific, and mathematical subprograms)3.
mathproc.for was developed using the
Silverfrost Plato IDE
on an AMD Athlon II X2 running WinXP Pro SP3. Its various
subprograms have been successfully called by FORTRAN, D,
Object Pascal, and Lazarus (using an
Object Pascal proxy) programs4.
The Simulated Annealing
subroutines (original FORTRAN source code published in
Numerical Recipes: The Art of Scientific Computing 1986)
were modified by breaking DE (difference in cost due to some change)
into
path cost change DP and extended cost change DE (this also required
adding μ, an extended cost associated with each node; this
concept was discussed in
Numerical Recipes: The Art of Scientific Computing but not
implemented).
DP =
√ ( (Xi
- Xi+1)2 + (Yi
- Yi+1)2 )
DE = (μi - μi+1)2
Total Cost Change = DP + DE
(The array IORDER(i) is used as an index into the X(i),
Y(i), and MU(i) arrays; only the elements in the
IORDER(i) array are modified. X(i) elements are
referred to as X(IORDER(i)); the same applies to the
Y(i) and MU(i) arrays.)
Also added another variable, IERR, to the parameter list;
IERR is a returned error code.
Each of these subroutines are called by the D procedure
dANNEAL (...) (or the FORTRAN subroutine
ANNEAL (...)5,
also contained in mathproc.for; used for testing).
Only the subprogram statement and variable declarations
are shown to prevent a possible intellectual property violation,
since the original FORTRAN source code is published. The unmodified
Numerical Recipes Simulated Annealing FORTRAN source code is
available for purchase at
Older Numerical Recipes book editions6
(the 1986 edition is not available online).
A student version of
Numerical Recipes In 'C': The Art Of Scientific Computing, Second Edition, © 1988-1992
is available from
PennState
at no cost.
Function
RAN3 (...) is a Portable Random Number Generator (machine
independent random number generator for consistent results on
different platforms) from
Numerical Recipes: The Art of Scientific Computing (1986). Used by
dMETROP (...) (Metropolis Algorithm) and dANNEAL (...);
Also called from Free Pascal Library
nrlazrs
function fRandom (...)
.
SAVE store variables statically. Static variables
retain their values until main program execution terminates.
Necessary to retain values of INEXT, INEXTP, and
array MA(i) between calls.
Simulates a coin toss by randomly returning 0 or 1.
Also called from Free Pascal Library
nrlazrs
function fRandom (...)
.
Function to find the distance between two points
Function subprogram RLEN (...) replaces the
Arithmetic Function (or Statement Function)
Note that the function RLEN (...) is declared as a variable. This
is required since mathproc.for is compiled with
IMPLICIT NONE
(Project, Properties, Compiler Options, Language, set global
IMPLICIT NONE).
dnrprocs dANNEAL (...) (or mathproc
ANNEAL (...) in an all FORTRAN solution) initializes the path
cost using RLEN (...), then begins its cycle:
using RAN3 (...), select a segment of 3 or more nodes;
simulates a coin flip with IRBIT1 (...) to decide whether to call
TRNCST (...) (difference in cost if the segment is moved) or
REVCST (...) (difference in cost if the segment is reversed);
dnrprocs dMETROP (...) (or mathproc
METROP (...) in an all FORTRAN solution) (both of which also
calls RAN3 (...)) is then called to
decide whether to perform the segment move or reversal. If yes,
either TRNSPT (...) or REVERS (...) is called to actually move or
reverse the segment.
Calculating DP using RLEN (...), calculating DE:
DP = 0.0 - RLEN(XX(1),XX(3),YY(1),YY(3),0.0,0.0) - . . .
+ RLEN(XX(1),XX(4),YY(1),YY(4),0.0,0.0) + . . .
DE = 0.0 - (MMU(3) - MMU(1))**2 - . . .
+ (MMU(4) - MMU(1))**2 . . .
(subtract connection, add reverse connection; similar calculation in
TRNCST (...) but with different subscript values)
etc.),
IERR is set to a non-zero value and subroutine immediately
exits. As an example, the code snippet above right is from
The original Numerical Recipes (1986) FORTRAN
source code did not have elaborate error checking. Added IERR to
the original parameter list. If the subroutine detects an error condition
(array subscript out of bounds,
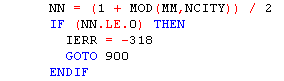
The FORTRAN .dlls (sttstcs.dll and mathproc.dll)
called by Fujitsu COBOL, D, Free Pascal, and
Lazarus programs were compiled with
a CheckMate Win32 configuration.
With a CheckMate Win32 configuration compiler includes code
to perform
run-time checking for any undefined variables or array elements in
+ - / * or ** arithmetic expressions; .NE. .EQ. etc. relational
expressions; .AND. .OR. etc. logical expressions; array subscripts;
etc.
Project Properties (mathproc.ftn95p),
Compiling, Linking:
Use the same Compiler Options, Miscellaneous as in compiling
the
sttstcs.dll
(Output filename, Output filetype, and Alternative compiler options)
Use the same Linker Options as in
sttstcs.dll
(Export all).
When passing numeric constants from one FORTRAN subroutine to
another, may need to set the default INTEGER and REAL kind using
Project, Properties, Compiler Options,
Numerical.
INTEGER kind 2 corresponds to INTEGER*2.
REAL kind 1 corresponds to REAL (or REAL*4).
Required for mathproc.for since subroutines TRNCST (...) and
REVCST (...) both pass constant zero to RLEN (...)
Project, Properties, Compiler Options,
Numerical
Compile and link normally using the Silverfrost FTN95 compiler
and SLINK
(Project, Set Target, DLL;
Build, Build) to create
mathproc.dll.
.LIB file (MATHPROC.LIB import library):
Depending on the calling program language, may need to use either
Silverfrost Plato SLINK or DMD utility implib
to build mathproc.lib.
(Free Pascal and
Lazarus
linking does not require a user generated mathproc.lib)
To use the Silverfrost Plato SLINK to build a Microsoft 32 bit
Linker compatible (Microsoft's own variant of the COFF format)
MATHPROC.LIB:
click Project, Set Target
click the LIB radio button
click OK
click Build, Build
Digital Mars compilers use a different object and import library file
format (Intel 32 bit OMF object and library file format)
than Microsoft's 32 bit tools (the .dll's produced are
compatible). Therefore, for Digital Mars D main programs and .dll's,
use the Digital Mars
implib utility (file bup.zip)
to create a DMD compatible mathproc.lib.
implib mathproc.lib mathproc.dll
in a MS-DOS command prompt
(batch file rrr.bat uses
short file names
to change to directory
C:\Documents and Settings\Rodney Roberts\My Documents\progProjects)
(Be sure to use the D2 32-bit Command Prompt for compatibility
with the CheckMate Win32 configuration,
Free Pascal,
and
Lazarus)
1. Press, William H., Brian P. Flannery, Saul A Teukolsky, and William T. Vetterling (1986). Numerical Recipes: The Art of Scientific
Computing. New York:Press Syndicate of the University of Cambridge.
More recent editions available at Numerical Recipes
2. Simulated Annealing, also known as the traveling salesman problem, is used for combinatorial minimization. The traveling salesman
problem involves a salesman who must travel to a large number of cities (or nodes, represented by X Y coordinates). What is the shortest
path the salesman can traverse visiting these cities? In a very large 'solution space', there are some solutions that are 'low cost'
(global minima) relative to other solutions. Simulated annealing searches for these 'low cost' solutions. Simulated annealing has also been
applied to designing integrated circuits. The traveling salesman problem is a NP-Complete problem (nondeterministic polynomial), where
N equals the number of nodes (or cities), and the computation time is proportional to eN.
3. Mathematical Procedures - FORTRAN Files (or more simply, mathproc.for) contains over 60 engineering, mathematical, and scientific
application subprograms (both functions and subroutines), many from Numerical Recipes: The Art of Scientific Computing, others are
from FORTRAN for Engineering 1972, FORTRAN For Scientists & Engineers 2nd Edition 1995, algorithms used in
Calculating the Center of Pressure, and others. This page focuses on the FORTRAN Simulated Annealing subprograms from
Numerical Recipes. Four root finding subprograms (see note 6 below) are from published algorithms, source available below.
4. As mentioned on other pages, when calling a FORTRAN subprogram from a FORTRAN, Fujitsu COBOL, or Free Pascal program,
the arguments are passed in normal order. When called from a D program, the arguments are passed in reverse order.
|
5. Not shown above are subroutine |
 |
argument list. Used different names for
and/or calling conflicts.
6. Source code for point rotation, triangular segment area, and four root finding subprograms in mathproc.dll not published in
Numerical Recipes 1986, FORTRAN for Engineering 1972, or FORTRAN For Scientists & Engineers, 2nd Edition, 1995 available.
The root finding subprograms focus on Polynomial Root finding. Includes Cubic Polynomial Roots - X3 + A1*X2 + A2*X + A3 = 0
(algorithm only published) from p. 146 in Numerical Recipes (1986). Source code includes source of algorithms.

